En differentialkvotient beskriver en grafs hældning i et givent punkt. Til at indtroducere differentialkvotienten indfører vi et begreb der hedder funktionstilvækst. Til at eksemplificere det definererer vi en funktion f(x) der afhænger af en værdi x. Vi kan altså sætte et x ind, og vi får f(x) retur. Feks. f(x) = 2x + 10 hvor x = 5 giver f(5) = 2 ⋅ 5 + 10 = 20. Hvis vi så også finder f(10) = 2 ⋅ 10 + 10 = 30, kan vi regne os frem til væksten der er sket mellem de to fundne værdier, den må være f(10) - f(5) = 30 - 20 = 10. Med det kan vi faktisk slutte os til at for hver fem skridt vi går hen ad x-aksen, stiger funktionsværdien med 10. Da vi er interesseret i en kvotient, kan vi opstille brøken: $$\frac{f(10) - f(5)}{10 - 5} = \frac{30 - 20}{10 - 5} = \frac{10}{5} = 2$$
der fortæller os, at hvis vi går ét skridt hen ad x-aksen, vokser funktionsværdien med 2. Og vi har fundet differentialkvotienten for f(x). Her er grafen:
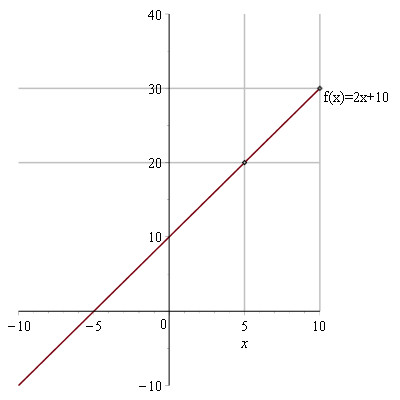
Funktionstilvæksten kan vi generalisere. I det ovenstående tilfælde er funktionen lineær, og en sådan funktion har altid en konstant differentialkvotient/vækst i alle punkter. Men hvis vi i stedet betragter et andengradspoynomie, bliver situationen lidt anderledes. Et andengradspolynomie har jo ikke samme hældning i alle punkter - faktisk har et sådan ikke samme hældning i to forskellige punkter overhovedet. For at regne differentialkvotienten til et andengradspolynomie kan vi starte med at skrive en funktionsværdi til et punkt z som f(z). Vi kan yderligere finde værdien til et punkt x som f(x). Med de to kan vi regne både tilvæksten på x-aksen: x - z og tilvæksten på y-aksen: f(x) - f(z), her tegnet i et koordinatsystem:
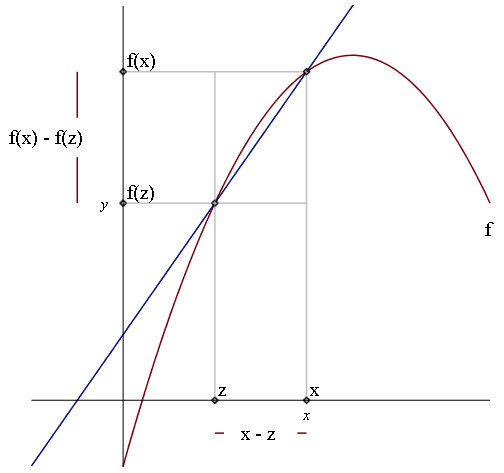
Det kan godt kræve lidt tilvænning at forstå tilvæksten, eller forskellene, mellem de to punkter (z,f(z)) og (x,f(x)). Som det ses, er der tegnet en blå graf gennem de to punkter, denne graf skærer grafen for f i de to punkter, derfor hedder den blå graf en sekant - sekanten er lineær. Det er vigtigt at bemærke at sekanten her er voksende. Det er ikke noget krav, den kan være både voksende, aftagende, og i dette tilfælde er den konstant hvis de to skæringspunkter befinder sig i samme højde på hver sind side af polynomiet. Hældingen på sekanten er givet ved følgende formel: $$h = \frac{f(x) - f(z)}{x - z}$$ Hvilket betyder, at hvis vi går et skridt hen ad x-aksen, stiger den blå graf med h. Det næste vi skal indføre, er en tangent. En sådan kan godt virke lidt som noget hokus pokus, men lad os se på den alligevel. Vi er nemlig interesseret i at finde f's hældning i ét punkt og ikke sekantens hældning i to. Derfor lader vi x gå mod z, dermed bliver afstanden mellem de to punkter sekanten skærer grafen for f i, mindre og mindre. Til sidst bliver den så lille, at vi kalder den for grænseværdien (betegnes lim) for hældningen til f i det givne punkt. Når det sker, siger vi at afstanden går mod 0, når x går mod z. Og når de to punkter er næsten lig med hinanden, siger vi at vi at sekanten er blevet til en tangent, den tangerer altså nu kun grafen i ét punkt.
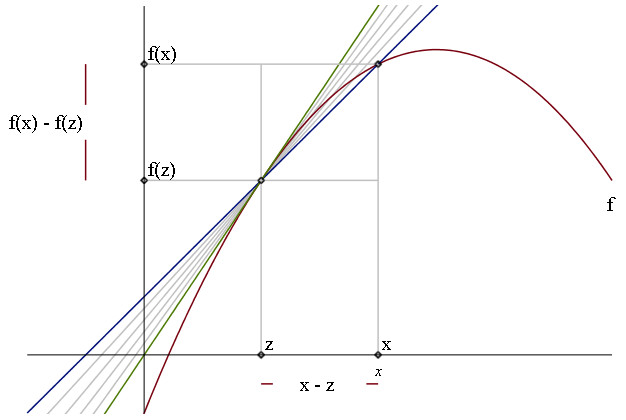
Her er tangenten den grønne linje. De grå linjer er sekanten der i dette tilfælde bliver stejlere og stejlere inden den bliver til tangenten når x går mod z. Vi kalder tangentens hældning i punktet z for f'(z), og vi skriver følgende som definition:
Antag at \(f\) er en funktion defineret omkring punktet \(z\) - altså at der findes et interval \(z - c \leq z \leq z + c\) hvori f er defineret. Hvis grænseværdien $$lim_{x \rightarrow z} \frac{f(x) - f(z)}{x - z}$$ eksisterer, er f differentiabel i punktet z, og vi kalder $$f'(z) = lim_{x \rightarrow z} \frac{f(x) - f(z)}{x - z}$$ for f's differentialkvotient i punktet z.
f'(x) betegner altså den mere generelle afledte funktion til f(x), og f'(z) betegner f(x) hældning i punktet z.
Med definitionen kan vi i tre trin vise hvordan den afledte til en funktion findes:
Trin1
Beregn funktionstilvæksten, og det gør vi sådan her:
$$f(x) - f(z) = ax^{2} + bx + c - (az^{2} + bz + c) =$$
$$ax^{2} + bx + c - az^{2} - bz - c =$$
$$ax^{2} - az^{2} + bx - bz =$$
$$a(x^{2} - z^{2}) + b(x - z) =$$
$$a(x - z)(x + z) + b(x - z)$$
Til den sidste omskrivning er der brugt en kvadratsætning. Dette vil come in handy ved næste skridt som er:
Trin2
Beregn sekanthældningen:
$$\frac{f(x) - f(z)}{x - z} =$$
$$\frac{a(x - z)(x + z) + b(x - z)}{x - z} =$$
$$a(x + z) + b$$
Trin3
Vi undersøger grænseværdien når x går mod z, ved simpelthen at lade x = z:
$$lim_{x \rightarrow z} \frac{f(x) - f(z)}{x - z} = a(z + z) + b = a2z + b = 2az + b$$
som er differentialkvotienten f'(z) til f(x) i punktet z. Da z kan være et hvilket som helst tal f(x) er defineret på, som i dette tilfælde er et hvilket som helst reelt tal, kan vi skrive f'(x) = 2ax + b som den afledte til f(x). Den afledte er altså en funktion der hermed er bevist.
At vi kan lade z = x, skyldes først og fremmest at har regnet brøken væk i trin2. Vi må IKKE dividere med 0! Men der er også andre forhold vi må tage når vi skal finde en grænseværdi.Dem ser vi nærmere på senere.
BEMÆRKNING
To andre måder at angive den afledte til f er:
Vi fortsætter og viser 2 af de andre elementære funktioners afledte på samme måde.
$$f(x) = \frac{1}{x}$$ $$f'(x) = \frac{-1}{x^2}$$
Trin1
Vi beregner funktionstilvæksten:
$$f(x) - f(z) = \frac{1}{x} - \frac{1}{z}$$
Trin2
Vi beregner sekanthældningen, og her må vi antage at x, z ≠ 0, og at x ≠ z:
$$\frac{f(x) - f(z)}{x - z} = \frac{1/x - 1/z}{x - z} = \frac{-1(-1/x + 1/z)}{zx(1/z - 1/x)} = \frac{-1}{zx}$$
Trin3
Vi finder grænseværdien når x går mod z ved at lade x = z:
$$f'(z) = lim_{x \rightarrow z} \frac{-1}{zx} = \frac{-1}{z^2}$$
og vi har nu fundet den afledte til f(x) i punktet z som er
$$f'(z) = \frac{-1}{z^2}$$
hvor z er i f's definitionsmængde som er alle reelle tal undtagen 0. Vi kan altså skrive den afledte til f(x) som:
$$f'(x) = \frac{-1}{x^2}, x \neq 0$$
$$f(x) = \sqrt{c}$$
$$f'(x) = \frac{1}{2 \sqrt{x}}$$
Trin1
Vi finder funktionstilvæksten:
$$f(x) - f(z) = \sqrt{x} - \sqrt{z}$$
Trin2
Vi finder sekanthældningen (igen ved brug af en kvadratsætning), og her må vi antage at x, z > 0, og at x ≠ z:
$$\frac{f(x) - f(z)}{x - z} = \frac{\sqrt{x} - \sqrt{x}}{x - z} = \frac{\sqrt{x} - \sqrt{z}}{(\sqrt{x} - \sqrt{z})(\sqrt{x} + \sqrt{z})} = \frac{1}{\sqrt{x} + \sqrt{z}}$$
Trin3
Vi lader x gå mod z og finder dermed grænseværdien:
$$f'(z) = lim_{x \rightarrow z} \frac{1}{\sqrt{x} + \sqrt{z}} = \frac{1}{2\sqrt{z}}$$
Den afledte er altså fundet og er
$$f'(x) = \frac{1}{2\sqrt{x}}, x \gt 0$$
for x i hele f's definitionsmængde som er alle positive reelle tal dog uden nul, derfor x > 0.
På samme måde kan vi vise den afledte til de andre elementære funktioner. Istedet for at gennemgå dem tre trin for hver, kan vi bare stille resultaterne op i en liste:
| f(x) | f'(x) |
| - | - |
| \(k\) | \(0\) |
| \(kx\) | \(k\) |
| \(x^{a}\) | \(a \cdot x^{a - 1}\) |
| \( \sqrt{x} \) | \(\frac{1}{2 \sqrt{x}}\) |
| \(\frac{1}{x}\) | \(\frac{-1}{x^2}\) |
| \(e^{x}\) | \(e^{x}\) |
| \(e^{kx}\) | \(ke^{kx}\) |
| \(a^{x}\) | \(a \cdot ln(a)\) |
| \(ln(x)\) | \( \frac{1}{x} \) |
| \(cos(x)\) | \(-sin(x)\) |
| \(sin(x) \) | \(cos(x)\) |
| \(tan(x)\) | \( \frac{sin^2(x) + cos^2(x)}{cos^2(x)}\) |
Med denne tabel kan vi regne os frem til hældningen for en given graf til en af de elementære funktioner i et givent punkt. Lad os sige at vi er givet funktionen $$f_{1}(x) = \frac{1}{x}$$ og et punkt z = 2. Vi skal finde hældningen på grafen i dette punkt som er: $$f_{1}'(z) = \frac{-1}{2^2} = \frac{-1}{4}$$
På samme måde kan vi finde hældningen i punktet z = 9 til grafen for: $$f_{2}(x) = \sqrt{x}$$ som findes ved: $$f_{2}'(z) = \frac{1}{2\sqrt{9}} = \frac{1}{2 \cdot 3} = \frac{1}{6}$$
...