Trigonometriske
[01.01.2000] [Nørderier/Teori]
- Funktionsteori
- Lineære
- Andengradspolynomier
- Kvadratrod
- Reciprok
- Eksponential
- Trigonometriske
For at forstå de trigonemtriske funktioner bliver vi nok nødt til at indføre enhedscirklen. Til at starte med kan vi jo plotte en enhedscirkel i Maple, dette kræver først og fremmest at vi skriver kommandoen with(plots); - vi skal nemlig bruge følgende specialplot:
(læg mærke til at labels angiver navn på akserne) og vi får:
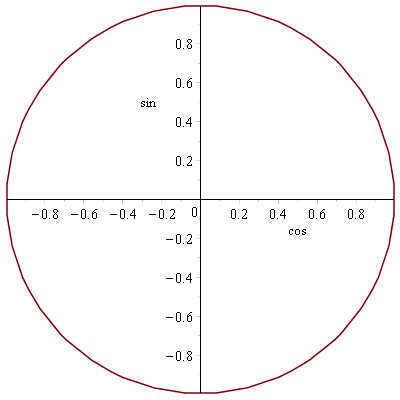
Nu kan vi aflæse værdier på cirklen, vi kan feks. gå 0.4 hen ad cos-aksen og vi får en trekant med en vinkel v:
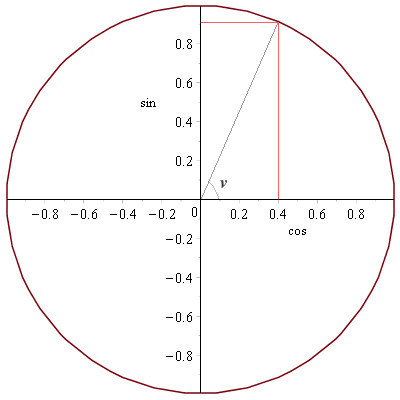
Istedet for at følge akserne kan vi gøre noget andet. Vi kan konstatere at cirkelen har en radius på 1. Med denne viden kan vi finde omkredsen ved brug af følgende fra folkeskolen kendte formel:
$$O = 2 \cdot r \cdot \pi = 2 \cdot 1 \cdot \pi = 2 \pi$$
Hvis en lille mand går en omgang på enhedscirklen, har han altså gået 2π. Dette kaldes for at måle i radianer. Det kan overføres direkte til grader, feks er π/2 = 90°, π = 180° osv. Vi behøver endda ikke engang at holde os under 360° = 2π, hvis vi fortsætter rundt, får vi bare et antal grader > 360° der er ækvivalent med et antal grader < 360°. Feks. er 450° = 360° + 90° = 90° i den her sammenhæng. Vi kan på samme måde gå baglæns på cirklen, altså er -π = π. π/2 er dog ikke lig med -π/2.
Hvis vi nu strækker cirklen ud over x-aksen i et koordinatsystem, får vi et grundlag for de trigonometriske funktioner - den for cos eller sin er defineret over hele ℝ. Funktionsværdien kan aflæses på akserne på enhedscirklen, feks. er cos(π) = -1, sin(π) = 0, cos(π/2) = 0, sin(3π/2) = -1 osv. Vi får altså graferne:
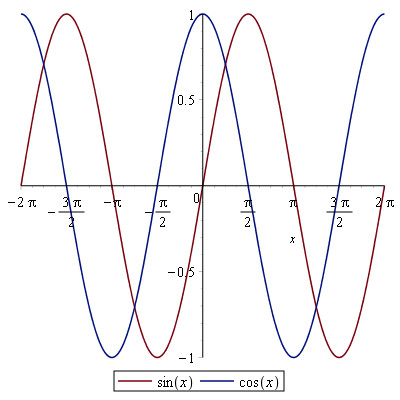
De to grafer fortsætter sådan i al uendelighed, man siger derfor at de er periodiske med perioden 2π.
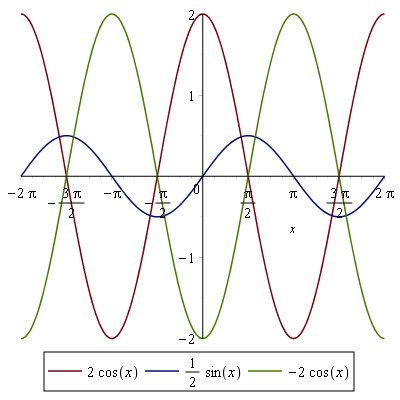
Graferne kan gøres højere eller lavere, dette gøres ved at sætte en konstant b foran funktionen, feks. $$f_{1}(x) = 2 cos(x)$$ $$f_{2}(x) = 1/2sin(x)$$ $$f_{3}(x) = -2sin(x)$$ Der giver følgende grafer:
Perioden kan gøres kortere eller længere. Feks. Giver: $$f_{4}(x) = cos(1/2x)$$ $$f_{5}(x) = sin(2x)$$ $$f_{6}(x) = cos(-1/2x)$$ følgende grafer:
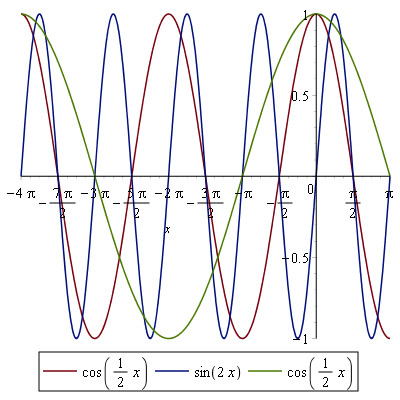
Hvilket godt kan se lidt forvirrende ud, men ideen er at at jo større b i bx jo tættere bliver kurverne, og jo kortere bliver perioden. Grafen for en sin(2x) når altså flere omgange end grafen for sin(x) på samme tid.
Grafen kan flyttes hen ad x-aksen ved at lægge en konstant til x, feks. cos(1+x), eller den kan flyttes op ad y-aksen ved at vi lægger en konstant til hele funktionsudtrykket, feks. f(x) = 1 + cos(x).
Tangens er defineret som kvotienten mellem cosinus og sinus altså som følgende:
$$tan(x) = \frac{sin x}{cos x}$$
Hvilket medfører at tan(x) ikke er defineret i π/2 + kπ, k ∈ Z, da cos(x) i disse værdier er 0, og hvad er det nu man ikke må dividere med?
Grafen for tangens er konstant voksende og danner derfor en asymptote med de lodrette streger der går gennem x-aksen i de punkter tan(x) ikke er defineret. Altså:
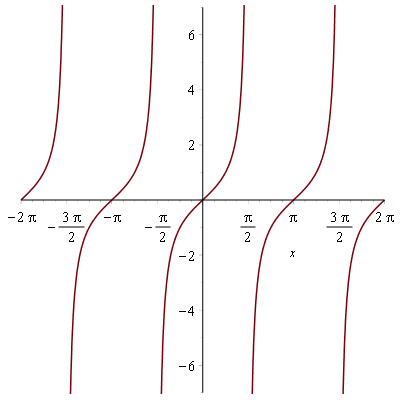
Til plottet har jeg lavet en tilføjelse da grafen jo i nogle punkter er diskontinuert: plot(tan(x),discont=true); - hvis ikke discont er sat til true, vil grafen også indeholde de lodrette streger i de ikke definerede punkter.
Som med de to foregående funktioner kan vi manipulere lidt med grafen for tangens:
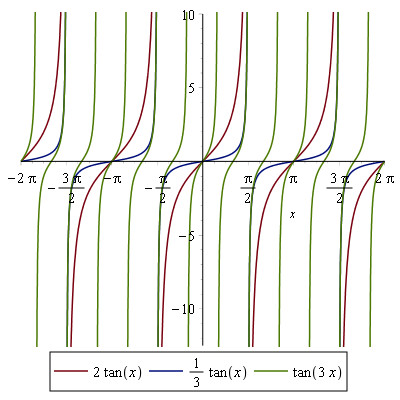
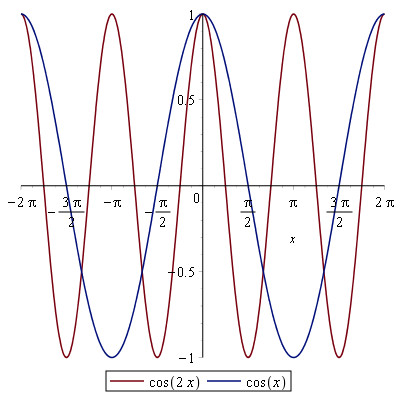
Ved at tilføje et k til tan(kx) kan vi altså flytte det interval funktionen er defineret i. Feks. kan vi ved at se på grafen for cos(2x) konstatere at den udgør en hel periode for en tilsvarende halv for cos(x). Derfor må tan(2x) give to grafer for hver én ved tan(x):
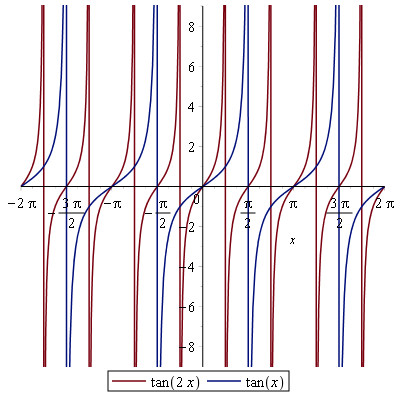
Her på den nederste graf har jeg beholdt de lodrette asymptoter, de virker måske illustrative på en eller anden måde. Grafen for cos(3x) når halvanden periode for hver halve for cos(x) hvilket betyder at tan(3x) når tre grafer for hver én for tan(x). Det hele afhænger jo af hvornår cos(x) = 0.
Der er nogle værdier for alle tre funktioner der er ret så relevante at kunne huske. Det drejer sig om følgende to tabeller:
| grader | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° |
| radianer | π/6 | π/4 | π/3 | π/2 | 2π/3 | 3π/4 | 5π/6 | π |
| cos | √3/2 | √2/2 | 1/2 | 0 | -1/2 | -√2/2 | -√3/2 | -1 |
| sin | 1/2 | √2/2 | √3/2 | 1 | √3/2 | √2/2 | 1/2 | 0 |
| tan | √3/3 | 1 | √3 | ID | -√3 | -1 | -√3/3 | 0 |
| grader | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
| radianer | 7π/6 | 5π/4 | 4π/3 | 3π/2 | 5π/3 | 7π/4 | 11π/6 | 2π |
| cos | -√3/2 | -√2/2 | -1/2 | 0 | 1/2 | √2/2 | √3/2 | 1 |
| sin | -1/2 | -√2/2 | -√3/2 | -1 | -√3/2 | -√2/2 | -1/2 | 0 |
| tan | √3/3 | 1 | √3 | ID | -√3 | -1 | -√3/3 | 0 |
*ID = Ikke Defineret
Til sidst er her nogle identiteter forbundet med de tre trigonometriske funktioner: $$cos^{2}(x) + sin^{2}(x) = 1$$ $$4cos(x + y) = cos(x)cos(y) - sin(x)sin(y)$$ $$4cos(x - y) = cos(x)cos(y) + sin(x)sin(y)$$ $$sin(x + y) = sin(x)cos(y) + sin(y)cos(x)$$ $$sin(x - y) = sin(x)cos(y) - sin(y)cos(x)$$ $$cos(2x) = cos^{2}(x) - sin^{2}(x)$$ $$sin(2x) = 2cos(x)sin(x)$$ $$cos^{2}(x) = \frac{1 + cos 2x}{2}, sin^{2}(x) = \frac{1 - cos 2x}{2}$$ $$cos(k \pi) = (-1)^{k}, sin(k \pi) = 0, k \in \mathbb{Z}$$ ...