Kvadratrod

[12.10.2020] [Nørderier/Teori]

• Funktionsteori
• Lineære
• Andengradspolynomier
• Kvadratrod
• Reciprok
• Eksponential
• Trigonometriske

Kvadratrodsfunktionen $$f(x) = \sqrt{x}$$ er specielt defineret i intervallet $$D_{f} = [0, \infty[$$ og har værdimængden $$V_{f} = [0, \infty[$$

Grafen kan altså på ingen måde ende i den negative ende af koordinatsystemet – så længe vi regner med reelle tal i hvert fald. Grafen er først stejl, men flader så mere og mere ud. Jo højere værdi \(k\) i \(\sqrt{kx}\), jo højere bliver grafen.

Her er et par eksempler på grafer:

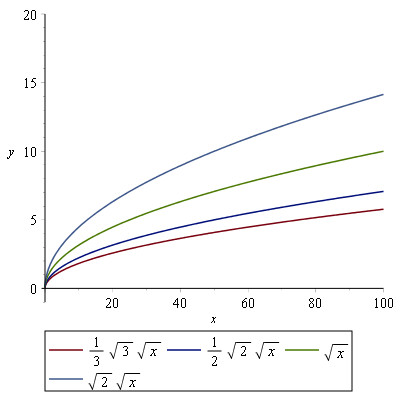
Der knytter sig en række regneregler eller identiteter til kvadratødder nemlig følgende: $$\sqrt{a b} = \sqrt{a} \sqrt{b} $$ $$\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}$$ $$a^{-1/2} = \frac{1}{\sqrt{a}} $$ $$ \sqrt{a} = a^{0.5} $$ $$ \sqrt{a^{2}} = \sqrt{a}^{2} = a $$ $$ \sqrt{a^{n}} = (a^{0.5})^n = a^{n/2} $$

Index Del