Andengradspolynomier
[12.10.2020] [Nørderier/Teori]
- Funktionsteori
- Lineære
- Andengradspolynomier
- Kvadratrod
- Reciprok
- Eksponential
- Trigonometriske
Andengradspolynomier er ret så centrale i matematik. De er generelt givet på formen: $$f(x) = ax^{2} + bx + c$$ hvor a ≠ 0 er andengradskoefficienten, b er førstegrads ditto, og c er en konstant. Hvis a = 0, er funktionen lineær. Som med lineære funktioner kan det godt betale sig at undersøge de forskellige komponenter i en andengradsfunktion for sig. Det mest simple andengradspolynomie er når både b = 0 og c = 0, da er funktionen givet ved \(f(x) = ax^{2}\). Vi kan udvælge nogle værdier for a, plotte dem i Maple og se hvad der sker:
f1:=x->4x^2; f2:=x->3x^2; f3:=x->2x^2; f4:=x->1/2x^2; f5:=x->-1/2x^2; f6:=x->-2x^2; f7:=x->-3x^2; f8:=x->-4x^2;Vi plotter med følgende kommando:
plot({f1(x), f2(x), f3(x), f4(x), f5(x), f6(x), f7(x), f8(x)}, legend = {4*x^2, 3*x^2, 2*x^2, (1/2)*x^2, -(1/2)*x^2, -2*x^2, -3*x^2, -4*x^2}, color = {blue, azure, purple, gray, green, olive, maroon, khaki}, labels = {x, y});Og vi får:
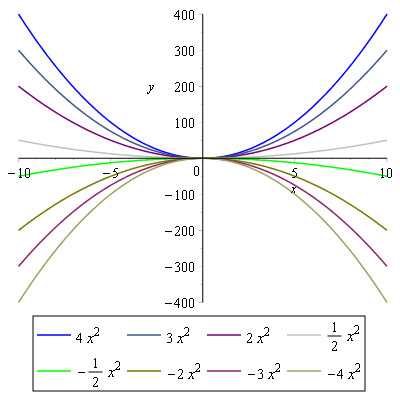
Det ses nu at:
For a > 0 vender parablens grene opad.
For a < 0 vender parablens grene nedad.
Og jo større |a| er, jo stejlere og smallere bliver parablen.
Grafen hedder en parabel da en parabel har den form, tænk evt. på en parabol. Alle typer af andengradsfunktioner er parabler når de tegnes i et koordinatsystem. Og der er det specielle ved parabler at de er symmetriske, en funktionsværdi har altså en tvilling untagen der hvor parablen er flad; dette punkt hedder toppunktet også i de tilfælde hvor det er det nederste punkt på grafen. Parabelformen gælder altså også for funkioner som \( f(x) = 2x^{2} - 3x + 10 \) eller \( f(x) = -3x^{2} - 4x + 2 \) og helt generelt for funkioner af formen \( f(x) = ax^{2} + bx + c \) - den form vi allerede har været inde på. De to andre koefficienter, b og c, har også en grafisk betydning. Den sidste værdi c er den værdi grafen skærer y-aksen i, ved alle de funktioner vi lige har tegnet, er c = 0, og alle graferne går gennem punktet (0,0). At c er skæringspunktet indses ved at sætte et \( x_{0} \) = 0 og så finde funktionsværdien: \( f(x_{0}) = a \cdot 0^2 + b \cdot 0 + c = c \). Pga. symmetrien har c-punktet en tvilling, medmindre det er toppunkt, hvis ikke, kan c-værdien bruges til at udlede en formel for toppunktet. Der er altså 2 steder hvor funktionsværdien er lig med c, det andet sted er et hvor \( x_{0} .ne 0 \), med denne viden kan vi isoloere c: $$ax_{0}^{2} + bx_{0} + c = c ax_{0}^{2} + bx_{0} = 0 \Rightarrow x_{0}(ax_{0} + b) = 0$$ Her kan vi indføre nulreglen, den siger, at for at et produkt af to tal skal give 0, må mindst en af tallene være 0. Da \( x_{0} \ne 0 \), må den anden faktor være lig med 0, altså er \( ax_{0} + b = 0 \) som kan omskrives: $$ ax_{0} + b = 0 \Rightarrow ax_{0} = -b \Rightarrow x_{0} = \frac{-b}{a} $$
Herfra er der blot tilbage at indse at toppunktet må ligge præcist midt mellem de to c-værdier, igen pga. symmetrien, vi finder altså ½ af \( x_{0} \) og får: $$ \frac{1}{2} \cdot x_{0} = \frac{1}{2} \cdot \frac{-b}{a} = \frac{-b}{2a} $$ y-koordinaten for toppunktet fås ved at indsætte ovenstående resultat som funktionsværdi, vi får da: $$ f(-b/2a) = \frac{-b^2 + 4ac}{4a} $$ Her kan vi indføre diskriminanten, den bliver brugt til at løse andengradsligninger, og formlen for diskriminanten er \( d = b^{2} - 4ac \). Vi indsætter diskriminanten og får:
Sætning 2
Toppunktsformlen. Grafen for andengradspoynomiet $$f(x) = ax^{2} + bx + c$$ har toppunktet med koordinaterne: $$\frac{-b}{2a} , \frac{-d}{4a}$$
Udover a- og c-værdien er der b-værdien. b-værdien siger noget om grafens hældning der hvor den skærer y-aksen. Værdien siger altså ikke noget om hvor det sker, men i stedet kun noget om hældningen i netop det punkt det sker i. For at få en forståelse af dette der rækker ud over en huskeregel, bliver jeg nødt til at indføre differentialregning, og det bliver først senere. Indtil videre må det være nok at huske på de 3 tildælde hvor b > 0, b < 0 og b = 0 givet ved følgende eksempler:
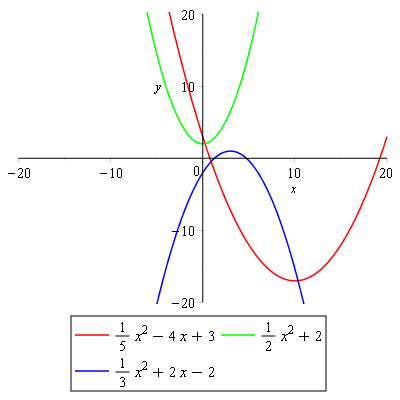
Den røde graf har b < 0, den grønne b = 0 og den blå b > 0.
Diskriminanten d der bruges til at løse andengradsligninger, kan også aflæses på grafen. Af det kommer:
Sætning 3
Om andengradspolynomiet $$f(x) = ax^{2} + bx + c$$ der har diskriminanten: $$d = b^{2} - 4ac$$ gælder at hvis d > 0, skærer parablen x-aksen i to punkter nemlig $$x = \frac{-b \pm \sqrt{d}}{2a}$$ hvis d = 0, skærer parablen x-aksen i et punkt nemlig toppunktet $$x = \frac{-b}{2a}$$ og hvis d < 0, skærer parablen ikke x-aksen.
Dette kan igen aflæses i et koordinatsystem:
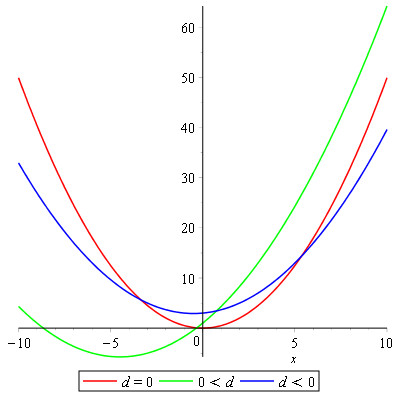
Samlet set kan vi altså få en idé af de forskellige værdier blot ved at se på grafen for en funktion:
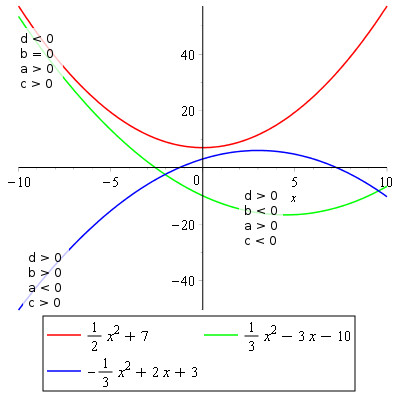
Til sidst skal vi lige se lidt på faktoropløsning. Hvis vi har et polynomie: $$f(x) = -x^{2} + 2x + 3$$ kan vi finde dets rødder ud fra formlerne i sætning 3:
Først finder vi diskriminanten: $$d = 2^{2} - 4 \cdot (-1) \cdot 3 = 4 + 4 = 4 + 12 = 16$$ Herefter finder vi rødderne: $$r_{1}, r_{2} = \frac{-2 \pm \sqrt{16}}{2 \cdot -1} \Rightarrow r_{1} = 3, r_{2} = -1$$ Disse to rødder kan indsættes i en faktoropløsning på følgende måde: $$-1(x + 1)(x - 3) = x^{2} - 3x + x - 3 = -1(x^{2} - 2x - 3) = -x^{2} + 2x + 3$$ Og første del er altså faktoriseringen af funktionen. Dette giver anledning til:
Sætning 4
For andengradspolynomiet $$f(x) = ax^{2} + bx + c$$ gælder at hvis d > 0 har polynomiet 2 rødder og faktoropløsningen:$$f(x) = a(x - r_{1})(x - r_{2})$$ hvis d = 0 har polynomiet én rod og faktoropløsningen: $$f(x) = a(x - r_{1})^{2}$$ hvis d < 0 har poynomiet hverken rødder eller faktoropløsning.
Beviset for sætning 4 er i to dele. Først ser vi på tilfældet d > 0. Vi vil gerne regne os fra faktoropløsningen og frem til den generelle formel for et andengradspolynomie: $$a(x - r_{1})(x - r_{2}) = a(x^{2} + r_{1}r_{2} - xr_{2} - xr_{1}) = a(x^{2} + r_{1}r_{2} - x(r_{2} + r_{1}))$$ De to rødder er jo giver ved formlen: $$r_{1} = \frac{-b + \sqrt{d}}{2a}, r_{2} = \frac{-b - \sqrt{d}}{2a}$$ Med dem kan vi regne først leddet \( x(r_{2} + r_{1}) \) : $$x({-b + \sqrt{d}}{2a} + \frac{-b - \sqrt{d}}{2a}) = x \cdot \frac{-2b}{2a} = x \cdot \frac{-b}{a}$$
(Husk på brøkregneregler). Produktleddet regner vi på samme måde: $$r_{1}r_{2} = \frac{-b + \sqrt{d}}{2a} \cdot \frac{-b - \sqrt{d}}{2a} = \frac{b^{2} - d}{4a^{2}}$$ (Her er brugt kvd.sætning 3, se længere nede, og en regneregel for kvadratrødder). Nu kan vi sætte hele smøren sammen: $$a(x^{2} + r_{1}r_{2} - x(r_{2} + r_{1})) = ax^{2} + ar_{1}r_{2} + bx$$ Det sidste vi skal undersøge, er altså leddet \(ar_{1}r_{2}\) . Hvis vi ganger a ind i brøken, får vi: $$a \cdot \frac{b^2 - d}{4a^2} = \frac{b^2 - d}{4a}$$ Herefter ser vi på formlen for diskriminanten \(d = b^{2} - 4ac \). Vi isolerer c: $$d = b^2 - 4ac \Rightarrow 4ac = b^2 - d \Rightarrow c = \frac{b^2 - d}{4a}$$ Og halleluja! Det ligner unægteligt at vi nu har følgende udtryk: $$ax^{2} + ar_{1}r_{2} + bx = ax^{2} + bx + c$$ For tilfældet d = 0 udleder vi formlen for andengradspolynomier stort set ved at benytte samme fremgangsmåde.
Som den totale afslutning på dette kapitel er her de ret så centrale, og vigtige at kunne bruge og genkende, kvadratsætniner givet som identiteter: $$(a + b)^{2} = (a + b)(a + b) = a^{2} + 2ab + b^{2}$$ $$(a - b)^{2} = (a - b)(a - b) = a^{2} + b^{1} - 2ab$$ $$(a + b)(a - b) = a^{2} - b^{2}$$ Etteren huskes som første led i anden plus andet led i anden plus det dobbelte produkt. Toeren huskes som det første led i anden plus det andet led i anden minus det dobbelte produkt. Den sidste som de to andre. Det er vigtigt at kunne regne begge veje, ofte er det faktisk det mest relevante at kunne regne fra højre mod venstre, feks. hvis vi er interesseret i at kunne regne med nulreglen.